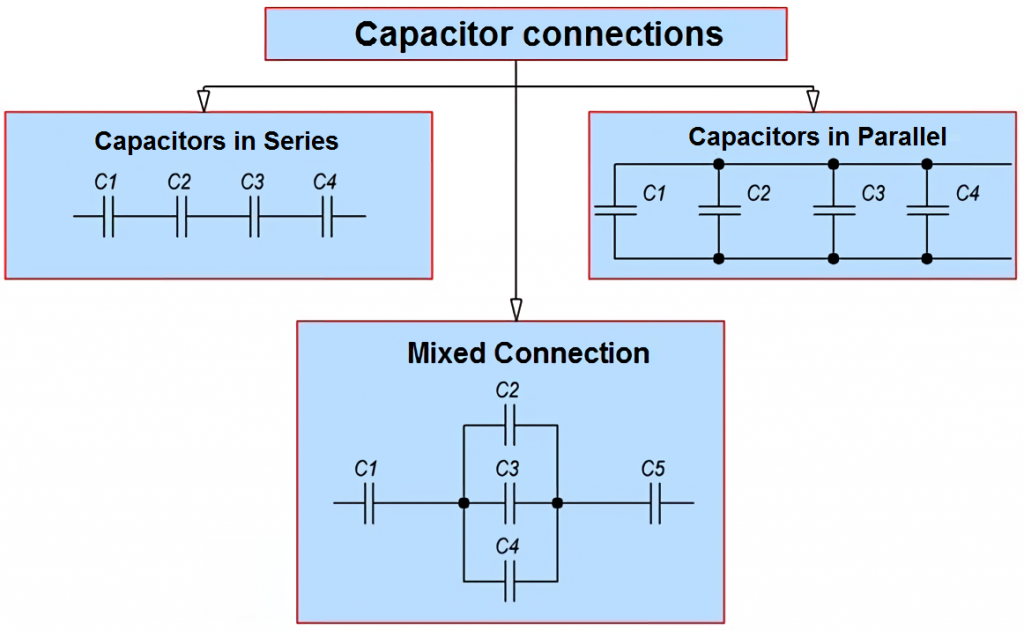
In electrical circuits, there are various ways of connecting capacitors. For example, capacitors can be connected in series, parallel, and parallel-series (the latter is sometimes called mixed capacitor connection). The available types of capacitor connections are shown in the figure below.
Capacitors in Parallel
Suppose a group of capacitors is connected in a circuit so that the plates of all capacitors are directly connected to the connection points. In that case, this connection is called a parallel connection of capacitors.
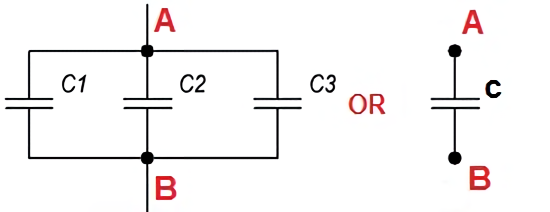
When a group of capacitors connected in parallel is charged, there will be the same potential difference between the plates of all the capacitors since all of them are charged from the same current source. Therefore, the total amount of electricity on all the capacitors will be equal to the sum of the amounts of electricity placed on each of the capacitors, as the charge of each of the capacitors occurs independently of the charge of the other capacitors of the group. On this basis, the entire system of capacitors connected in parallel can be considered as one equivalent capacitor. Then the total capacitance of the capacitors in parallel connection is equal to the sum of the capacitances of all connected capacitors.
Let us denote the total capacitance of the capacitors connected in a battery by the letter C, the capacitance of the first capacitor C1, the capacitance of the second capacitor C2 and the capacitance of the third capacitor C3. Then the following formula is valid for the parallel connection of capacitors:
С = C1 + C2 + C3 + … + Cn
The last + sign and the ellipsis indicate that this formula can be used for four, five, or any number of capacitors.
Capacitors in Series
If, however, the capacitors in a battery are connected in the form of a chain, and the plates of only the first and last capacitors are directly connected to the connection points in the circuit, such a connection of capacitors is called a series connection.
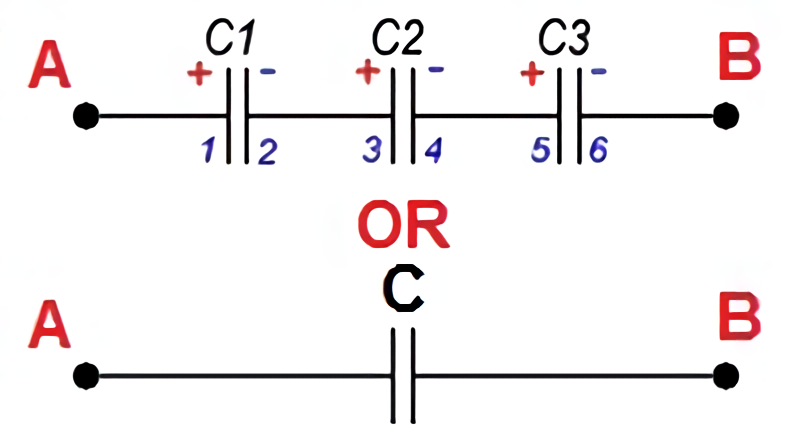
All capacitors are charged with the same amount of electricity in a series connection because only the outermost plates (1 and 6) are charged directly from the current source, and the remaining plates (2, 3, 4 and 5) are charged through the influence. The charge of plate 2 will be equal in magnitude and opposite in sign to the charge of plate 1, the charge of plate 3 will be equal in magnitude and opposite in sign to the charge of plate 2, etc.
The voltages on the different capacitors will generally be different because different voltages are always required to charge the same amount of electricity for capacitors of different capacities. The smaller the capacitance of a capacitor, the greater the voltage needed to charge that capacitor with the required amount of electricity, and vice versa.
Thus, when charging a group of capacitors connected in series, the capacitors of small capacitance will have higher voltages, and the capacitors of large capacitance will have lower voltages.
Similarly to the previous case, we can consider the whole group of capacitors connected in series as one equivalent capacitor, between the plates of which there exists a voltage equal to the sum of voltages on all capacitors of the group, and the charge of which is equal to the charge of any of the capacitors of the group.
Take the smallest capacitor in the group. It should have the highest voltage. But the voltage on this capacitor is only a fraction of the total voltage that exists on the entire group of capacitors. So the voltage on the whole group is greater than the voltage on the capacitor with the smallest capacitance. And hence it directly follows that the total capacitance of a group of capacitors connected in series is less than the capacitance of the smallest capacitor in the group.
It is most convenient to use the following formula to calculate the total capacitance of capacitors connected in series:
1/С = 1/C1 + 1/C2 + 1/C3 + … + 1/Cn
For the special case of two capacitors connected in series, the formula for calculating their total capacitance will be as follows:
С = C1 * C2/C1 + C2
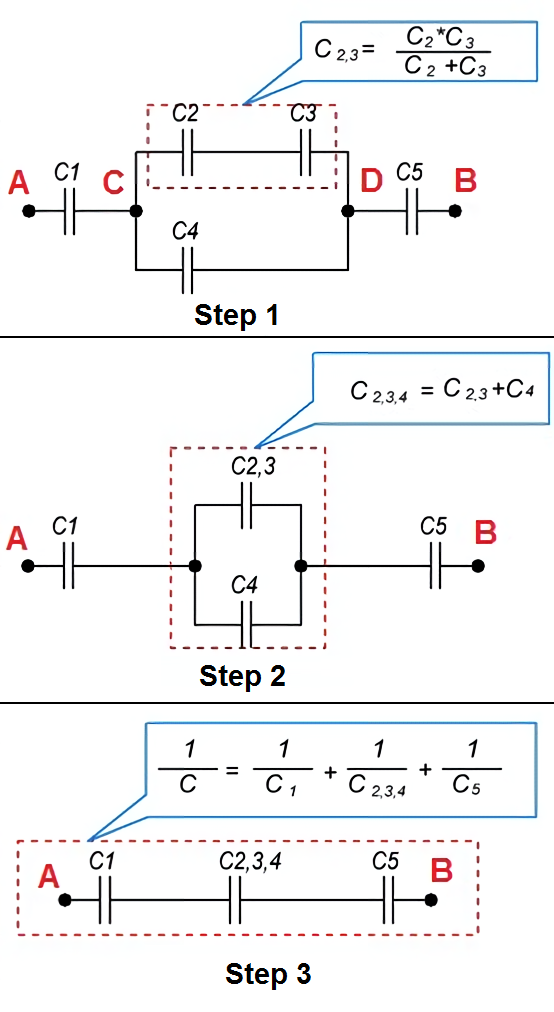
Series-Parallel (Mixed) Connection of Capacitors
A series-parallel connection of capacitors is a circuit that has sections of capacitors both in parallel and in series.
The illustration below shows an example of a mixed-capacitor circuit.
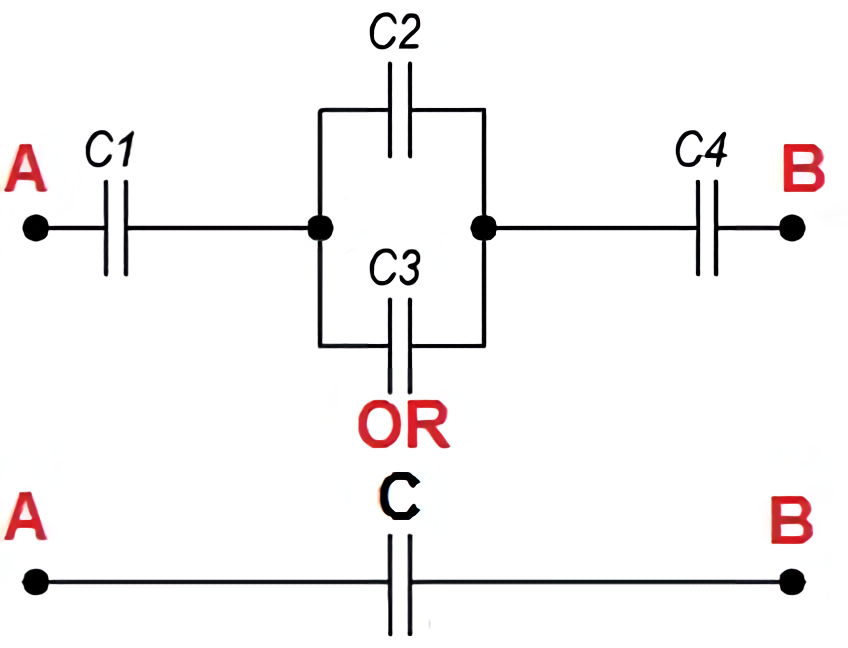
When calculating the total capacity of such a circuit section with a series-parallel connection of capacitors, this section is divided into the simplest sections consisting only of groups with series or parallel connections of capacitors. Further, the calculation algorithm is as follows:
- Determine the equivalent capacitance of the sections with a series connection of capacitors.
- If these sections contain capacitors connected in series, first calculate their capacitance.
- After calculating the equivalent capacitances of the capacitors, redraw the circuit. Usually, a circuit of equivalent capacitors connected in series is obtained.
- Calculate the capacitance of the resulting circuit.
One example of a mixed capacitance calculation is shown in the figure below.
More articles about capacitors:
- Electrolytic vs. Ceramic Capacitors: The Differences & Usage
- How to Test a Capacitor with a Multimeter
Related Video: Capacitors in Series and Parallel Explained!
Final Words
Now you know about the series, parallel and mixed connection of capacitors. Have you found this article useful? Or maybe you still have questions? Feel free to write in the comments!